අපි අද බලමු මොනවද මේ logic gate කියන්නෙ කියල. Digital electronics වල තියෙන සරලම කොටස තමයි මේ logic gates කියල හදුන්වන්නෙ. මේවත් හරියට අපි දන්න ගේට්ටු වගේ තමයි.ගේට්ටුව ඇරියොත් විතරයි අපට ඒ හරහා යන්න පුලුවන්කම ලැබෙන්නෙ. ඉතින් මේ ගේට්ටු ඇරගන්න තියන යතුර තමයි විදුලි බලය.මේ ගැන තව ඉස්සරහදි හොදට දැනගන්න ලැබෙයි. Logic gates යොදාගන්නව digital circuits නිර්මාණය කරන්න. ඔයාල දැනටමත් දන්නව Digital electronics වල තියෙන්නෙ binary number System එක කියල. ඒ කියන්නෙ 1 හා 0 කියන ඉලක්කම් දෙක විතරයි digital electronic use කරල හදපු devices වලට තේරෙන්නෙ.අපට මේක පැහැදිලි කරගන්න පුලුවන් පහල තියෙන පරිපථය බැලුවහම.
මේ තියෙන්නෙ ස්විව් එකක් දක්වන පරිපථ සටහනන් දෙකක් පළවෙනි එකේ ස්විච් එක off කරල තියෙන්නෙ(open කරල) දෙවනි එකේ ස්විව් එක on කරල තියෙන්නෙ (close කරල) පළමු අවස්ථාවෙදි switch එක හරහා විදුලිය ගමන් කරන්නෙ නෑ. නමුත් දෙවනි අවස්ථාවෙදි නම් විදුලිය ගමන් කරනව.අපි මේ විදුලිය ගමන් කරන අවස්ථාව 1 කියලත ගමන් නොකරන අවස්ථාව 0 කියලත් හදුන්වනව.
| අවස්ථාව | විදුලිය ගමන් කරයි/නොකරයි | ද්විමය අග |
| OFF | නොකරයි | 0 |
| ON | කරයි | 1 |
මතක තියාගන්න ඕන වැදගත්ම දේ තමයි විදුලිය ගමන් කරනව නම් 1 කියලත් එහෙම නැත්තම් 0 කියලත් කියන එක. Logic gates තියෙන්නෙ කොහේද? බලන්න පහළ තියෙන පින්තූරෙ දිහා මොකද්ද මේ තියෙන කලුපාට කෑල්ලඅපි මේකට කියනව integrated circuit කියල කෙටියෙන් IC කියල. හැම එකකම නොවුනත් මේ IC ඇතුලෙ logic gates අන්තර්ගත කරල තියෙනව.උඩ තියන පින්තූරෙ තියෙන්නෙ cd 4071 කියන නමින් හදුන්වන IC එක මේකෙ ඇතුලෙ මෙන්න මේ විදියට OR gate හතරක් අන්තර්ගත කරල තියනව.IC එකේ අග්ර වලට සම්බන්ධක යොදාගෙන මේව භාවිතා කරන්න පුලුවන්.
Logic Gates වර්ග. මෙතන ඉදින් අපි කතා කරන්නෙ logic gates වර්ග පිළිබදව.ප්රධාන වශයෙන් මූලික gates වර්ග තුනක් තියෙනව AND,OR හා NOT කියල මේ තුන මගින් තවත් gates 3 ක් නිර්මාණය කරල තියෙනව NAND,NOT හා XOR යන නම් වලින් දැන් එතකොට ඔක්කොම gates වර්ග 6 අපට අදුරගන්න පුලුවන්.පහළ රූපෙ තියනව ඒ ඒ gates වලට අදාල පරිපථ සලකුණු.
1. AND GATE AND GATES ගැන ඉගෙන ගන්න කලින් පහල තියෙන පරිපථය දිහා බලන්න.
c කියන බල්බ් එක දල්වන්න A හා B කියන ස්විව් දෙකම on කරන්න ඕන කියල
පේනව නේද? අන්න ඒ වගේ තමයි AND gate එකක් ඇරගන්න ස්විච් දෙකම 1 කරගන්න ඕන ඒ කිව්වෙ on කරගන්න ඕන.
උඩ තියෙනෙ And gate එකේ A හා B කියන්නෙ ස්විව් දෙකක් කියල නිකමට හිතන්නකො
එතකොට A ස්විව් එක on කරහම A කියන්නෙ 1 කියලත් හිතන්නකො B ත් on කර නිසා B
ගෙ අගයත් 1 කියල හිතන්න. A හා B දෙකම on උනොත් තමයි And වර්ගයේ ගේට්ටු
ඇරෙන්නෙ. දැන් y ගෙ අගයත් 1 මොකද දැන් ගේට්ටුව ඇරිල තියන නිසා ගේට්ටුව හරහා
යන්න ආපු අය ගේට්ටුව හරහා ඇවිත් නිසා.අපි දැන් ආයෙ අර කලින් And සදහා ගනිපු
circuit එක බලමු.මේක අවස්ථා 4 ක තියෙන්න පුලුවන් කියල පේනවද ?

A ස්විච් එක off(0) B ස්විච් එක off(0) A ස්විච් එක off(0) B ස්විච් එක on(1) A ස්විච් එක on(1) B ස්විච් එක off(0) A ස්විච් එක on(1) B ස්විච් එක on(1) A ස්විච් එක on(1) B ස්විච් එක on(1) කියන අවස්ථාවෙදි තමයි බල්බ් එක දැල්වෙන්නෙ.මේක gate එකටත් අදාලයි.
|
A
|
B
|
Z
|
|
ON |
ON |
1 |
|
ON |
OFF |
0 |
|
OFF |
ON
|
0
|
|
OFF |
OFF |
0 |
|
A
|
B
|
Z
|
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1
|
0
|
|
0 |
0 |
0 |
මෙතන තියෙන දෙවනි වගුවට අපි කියනව true tables කියල. gate එක තිබිය හැකි අවස්ථා තමයි මේ වගුවෙන් පෙන්නනෙ මේ වගුව දිහා හොදට බැලුවහම පේනව නේද A හා B ගෙ තියන අගයන් ගෙ ගුණිතයට Z සමාන වෙනව කියල.
- 1 * 1 = 1
- 1 * 0 = 0
- 0 * 1 = 0
- 0 * 0 = 0
හරිම සරලයි ඒ කියන්නෙ Z = A * B කියන එක. And gate එකක් දැකපු හැටියෙ මේක මතක් උනොත් හොදටම ඇති.මේ තියෙන්නෙ and ගේට් 4 ක් තියෙන IC එකක් 2. OR Gates
බලන්න මේ පරිපථය දිහා.
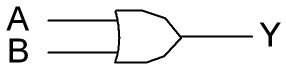
කලින් වගේම ස්විව් දෙකක් තියෙනව හැබැයි දෙකෙන් ඕනම එකක් on කරොත් බල්බ් එක පත්තු කරන්න පුලුවන් දෙකම off කරොත් විතරයි බල්බ් එක දැල්වෙන්නෙ නැත්තෙ. OR කියන වර්ගයේ ගේට්ටු ඇරගන්න එක ස්විච් එකක් on කරගත්තහම ඇති. බලන්න පහල තියෙන true table එක දිහා
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
මේ වගුවවෙත් රටාවක් පේනව නේද? A හා B ගෙ අගයන්ගෙ එකතුව නේද Y ට තියෙන්නෙ? 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 1 * ඔයාල බලයි 1 + 1 කොහොමද 2 නොවී 1 උනේ කියල මතක තියාගන්න 1 + 1 = 2 වෙන්නෙ දහයෙ පාදයෙ ඉලක්කම් වල බව අපි දැන් use කරන්නෙ දෙකේ පාදයේ ඉලක්කම්. දෙකේ පාදයෙන් 1 + 1 = 10 අපි අග තියන 0 ඉවත් කරල 1 + 1 = 1 කියල ලියනව. ඕන්න එහෙනම් OR GATE එකේ පොදු සමීකරණය තමයි A + B = Y
කියන එක.OR GATE එක දැක්ක ගමන් මේක මතක් වෙන්න ඕන.පහල තියෙන්නෙ or ගේට් තියෙන IC එකක්. 7432 කියන IC එක.
3.NOT GATE මේක තමයි තියෙන සරලම ගේට් එක.ඒ වගේම මේක ටිකක් අමුතුයි.මේ ගේට්ටුවෙන් කවුරු හරි යන්න ආවොත් ගේට්ටුව වැහෙනවා.ගේට්ටුව හරහා යන්න කවුරුත් නැත්තම් ගේට්ටුව ඇරිල තියෙන්නෙ. පිස්සු නේද ? ඒත් ඒ මේකෙ හැටි එහෙමයි.බලන්න පහල තියෙන පරිපථය.
මේකෙ තියන ස්විච් එක කලින් ඒවයෙ තිබුනට වඩා වෙනස් නේද? නිතරම පරිපථය සම්බන්ධවෙලාමයි තියෙන්නෙ.අපි ස්විච් එක press කරොත තමයි පරිපථය බිදිල බල්බ් එක දැල්වීම
නවතින්නෙ.
බලන්න true table එක හරිම සරලයි.
A Y 0 1 1 0
A ගෙ අනුපූරකය එහෙමත් නැත්තම් විරුද්ධ එක තමයි Y ට ලැබෙන්නෙ.ඒක මෙන්න මේ විදියට ලියන්න පුලුවන්.
A = Y'4. NAND GATE මම මුලින්ම කිව්වනෙ AND , OR හා NOT කියන මූලික ගේට් වලින් තමයි අනිත් Gates නිර්මාණය වෙලා තියෙන්නෙ කියල ඉතින් NAND gate එක හදල තියෙන්නෙ AND හා NOT ගේට් දෙක එකට බද්ධ කරල බලන්න පහල තියෙන රූපෙ.
දෙවනි එකේ තමයි නියම සලකුණ බොලෙන් තමයි අදුරගන්නෙ not එකක් තියෙනව කියල.AND ගේට් එකේ output එක AB කියල මතකයි නෙ ඒක ආයෙමත් NOT එකක් හරහා ගියහම AB' වෙනව.මේක හොදට තේරුම් ගන්න පුලුවන් true table එක බැලුවහම.
| A | B | AB | AB' |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
මේ table එකේ පියවර දෙකට දක්වල තියෙන්නෙ AB කියන්නෙ AND ගේට් එකේ
output එක.
| A | B | Y' |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
මේකෙ සමීකරණේ තමයි (A * B)' = Y A * B ගෙ සම්පූර්ණ ගුණිතය තමයි y ට සමාන වෙන්නෙ.මේ ගේට් එක මතක තියා ගන්න එක සමාන input එකක් දුන්නොත් තමයි ගේට්ටුව වැහෙන්නෙ කියල.
NOR GATE මේකත් හැදිල තියෙන්නෙ OR හා NOT ගේට්ටු දෙකක එකතුවීමෙන්.A හා B අගයන් දෙක OR ගේට් එක මගින් එකතු කරල දෙකකොට not එක මගින් ඒක කනපිට
හරවන එක තමයි කරන්නෙ.true table එක මෙහෙමයි.
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
සමීකරණෙ මෙහෙමයි (A + B)' = Y
input එකට 1 ගෑවිලාවත් තිබුනොත් output එක 0 වෙනව කියල මතක තියාගන්න.XOR Gate මේක තමයි අන්තිමට ඉගෙන ගන්න තියෙන gate එක ඒ වගේම තියෙන වෙනස්ම විදියෙ gate එක තමයි මේක.මේකෙන් වෙන වැඩේ ලේසියෙන් මතක තියාගන්න පුලුවන් මේ විදියට එකිනෙකට අසමාන input ලබා දුන්නොත් output එක 1 වෙනව. Input දෙක සමාන නම් output එක 0 වෙනව. මේකෙ true table එක එන්නෙ මෙහෙමයි.
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
මතක තියා ගන්න මේකෙ සමීකරණෙ AB' + A'B = y
මේ තියෙන්නෙ XOR ගේට් තියෙන IC එකක්.අපි දැන් ඉගෙන ගනිපු gates වල කියාකාරීත්වය තව දුරටත් පැහැදිලි කරගන්න මෙන්න මේ
web site එකට යන්න
http://www.neuroproductions.be/logic-lab/index.php?id=52
මෙතන තියෙන ඒව ඇත්ත gates වගේම ක්රියා කරනව. ඔන්න දැන් පාඩම නම් ඉවරයි මම
හිතනව කට්ටිය යම් දෙයක් ඉගෙන ගන්න ඇති කියල. පොඩ්ඩක් මොලේ කල්පනා කරොත්
අපට පුලුවන් මේව ප්රයෝගික දේවල් සදහා යොදා ගන්න පුලුවන්. කමෙන්ට් එකක් දාල
යන්න අමතක කරන්න එපා.










2 comments:
මේක නම් ගොඩක් වටිනවා. මට ලොජිකල් ගේට්ස් නිකං ග්රීක් වගේ වෙලා තිබුනෙ. මේකෙන් තමයි මම වැඩේ අල්ල ගත්තෙ. එල.. නියමයි. (y)
නියමයි සහෝ .. දිගටම කරගෙන යමු .. ඔබට යහපතක්ම වේවා ... සියලු කටයුතු සාර්ථක වේවා ...
Post a Comment